Conceptos
- Comparar y ordenar fracciones y números mixtos
Recuerda que números mixtos (fracciones mixtas) están formados por un número natural y un fraccionario. Todas las fracciones mayores que la unidad se pueden expresar en forma de número mixto.
Convertir una fracción impropia a número mixto por ejemplo
. Dividimos 8:5=1 y el resto es 3. Por tanto 1 es el número natural, 3 es el numerador de la fracción y el denominador no cambia, es decir es 5. 
. Dividimos 8:5=1 y el resto es 3. Por tanto 1 es el número natural, 3 es el numerador de la fracción y el denominador no cambia, es decir es 5.
Convertir número mixto a fracción impropia: Para convertir el número mixto en fracción debemos multiplicar el número natural por el denominador de la fracción y sumar el numerador al resultado. Por ejemplo 
= ¿?; (1+5) +3 = 
; 
= ¿?; (1+5) +3 = ; - Número mixto y una fracción propia
Cuando comparamos una fracción propia y un número mixto, la fracción propia siempre será menor.
- Número mixto y una fracción impropia
Si estamos ante una fracción impropia, es conveniente convertir la fracción impropia en número mixto.
Cuando tenemos dos números mixtos, primero nos fijamos en el entero y luego en la fracción.
- Comparar y ordenar fracciones
Hay distintas formas para comparar y ordenar fracciones, dependiendo del tipo de fracción:
- Fracciones con igual denominador
De dos fracciones que tienen el mismo denominador es menor la que tiene menor numerador.
- Fracciones con igual numerador
De dos fracciones que tienen el mismo numerador es menor el que tiene mayor denominador.
- Con numeradores y denominadores distintos
Para comparar fracciones que tienen distintos denominadores y distintos numeradores, puedes seguir los siguientes pasos:
Paso 1:
Encontrar fracciones equivalentes a las fracciones dadas, donde ambas tengan el mismo denominador.
Paso 2:
Comparar los numeradores de las fracciones encontradas.
Resolución
- Fracciones con igual denominador
¿Qué fracción es menor?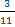 
; 
;
Al tener el mismo denominador, comparamos los numeradores.
3 < 5, (3 es menor), por tanto 
< 
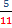(3/11 es menor).
< (3/11 es menor).
- Fracciones con igual numerador
¿Qué fracción es menor?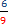 
; 
;
Al tener el mismo numerador, nos fijamos en los denominadores
< 
(
,al tener mayor denominador, la fracción es menor porque se divide en más partes más pequeñas).
,al tener mayor denominador, la fracción es menor porque se divide en más partes más pequeñas).- Con numeradores y denominadores distintos
¿Qué fracción es menor?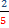 
; 
;
Paso 1:
- Hallamos el común denominador de
y
Calculamos mínimo común múltiplo entre los denominadores
Múltiplos de 5: 5, 10, 15, 20, 25, 30, 35, 40, 45,
Múltiplos de 7: 7, 14, 21, 28, 35, 42, 49….
m.c.m (5 y 7) = 35
m.c.m = común denominador
Común denominador de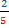 
y 
= 
y 
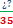y = y - Hallamos el numerador de cada fracción
 | |
Paso 2:
Comparamos los numeradores de las fracciones.
14 < 15, por tanto 
< 
<
Vídeo explicativo
Ejemplo de la vida real
Antonio y Belén fueron a comprar un poco de tarta de queso a la tienda de al lado de su casa. Antonio compró 9/12 de tarta y Belén 7/10 de otra tarta de igual tamaño que la de su amigo. ¿Quién compró más cantidad?
Resolución
Reducir la fracción a común denominador para poder comparar las fracciones 
Método mínimo común múltiplo
Paso 1:
Obtener común denominador de 
- Hallar mínimo común múltiplo (m.c.m)
Múltiplos de 12: 12, 24, 36, 48, 60, 72, 84
Múltiplos de 10: 10, 20, 30, 40, 50, 60, 70, 80
m.c.m de 12 y 10: 60
Paso 2: Hallar numerador de las fracciones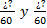 
.
.
Resultado es 
y 
y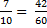
Si Antonio compró 
y Belén 
, ¿quién compró más cantidad?
y Belén , ¿quién compró más cantidad?
Hemos calculado que Antonio compró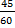 
de tarta y Belén 
.
de tarta y Belén . 
, con lo cual, Antonio compró más cantidad.
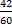Método de productos cruzados
Paso 1:
Multiplica la primera fracción por el denominador de la segunda y después multiplica la segunda fracción por el denominador de la primera.
Paso 2:
Simplifica. Las dos fracciones se pueden dividir entre 2
Hemos calculado que Antonio compró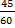 
de tarta y Belén 
.
de tarta y Belén . 
, con lo cual, Antonio compró más cantidad. Llegamos al mismo resultado.
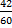Enlaces de interés:
https://es.khanacademy.org/math/cc-fourth-grade-math/cc-4th-fractions-topic/cc-4th-mixed-numbers/e/comparing_improper_fractions_and_mixed_numbers
gracias!
ResponderEliminar