Conceptos
¿Cómo podemos obtener fracciones irreducibles? Antes de empezar, vamos a ver qué son fracciones irreducibles.
Fracción irreducible: Se llama fracción irreducible a la fracción que no se puede simplificar más.
Simplificar (o reducir) una fracción: significa hacer la fracción lo más simple posible.
Hay dos maneras para llegar a una fracción irreducible (reducir una fracción a su mínima expresión).
Método de divisiones sucesivas
Divide el numerador (números de arriba) y el denominador (números de abajo) a la vez por aquel divisor que los dos tengan en común (factor común) Ambos deben dividirse por el mismo número o divisor a la vez.
Recuerda que los divisores de un número son aquellos que al dividir el número, el resto es 0. Por ejemplo los divisores de 12 son: 1, 2, 3, 4, 6 y 12. Si se divide 12 por cualquiera de ellos el resto es 0.
Repite el proceso hasta que no tengan ningún divisor común, salvo el número 1.
Método del máximo común divisor
Paso 1
Hallamos el máximo común divisor
Recuerda que el Máximo Común Divisor (M.C.D) de dos o más números es el mayor de los divisores comunes a estos números. Por ejemplo los divisores de 12 son 1, 2, 3, 4, 6 y 12 y los divisores de 24 son 1, 2, 3, 4, 6, 12 y 24. Los divisores comunes de 12 y 24 son 1, 2, 3, 4, 6, y 12. El mayor de ellos es el 12, por tanto, el 12 es el Máximo Común Divisor.
Paso 2
Dividimos el numerador y denominador entre el máximo común divisor (M.C.D)
Resolución
¿Cómo simplificar una fracción?
Simplificamos la fracción  (36/60)
(36/60)
Método de divisiones sucesivas
Buscamos el divisor común. Ya que son números pares, lo más sencillo es empezar por el 2.
Dividimos tanto el numerador como el denominador entre 2
El resultado es 18/30
Vemos que podemos seguir con el proceso, ya que todavía tienen divisores en común. Todavía se pueden dividir entre 2.
Dividimos otra vez el numerador y denominador entre 2
El resultado es 9/15
Comprobamos de nuevo si tienen divisores en común. Vemos que tanto el 9 como el 15 se pueden dividir entre 3.
Dividimos el numerador y denominador entre 3
La fracción irreducible es  , ya que no podemos simplificar (reducir) la fracción más. El único divisor que tienen en común es 1.
, ya que no podemos simplificar (reducir) la fracción más. El único divisor que tienen en común es 1.
Método del máximo común divisor
Paso 1
Buscamos el máximo común divisor (M.C.D)
- Primero localizamos los divisores de cada uno de los números (36 y 60).
Divisores de 36 son 1, 2, 3, 6, 12, 18 y 36.
Divisores de 60 son 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60.
- Ahora comprobamos ¿Qué divisores tienen en común estos números?
Los divisores comunes de 36 y 60 son 1, 2, 3, 6 y 12.
El mayor de ellos es 12, con lo cual el máximo común divisor (M.C.D) de 36 y 60 es 12.
Paso 2
Dividimos tanto el numerador (36) como el denominador (60) entre m.c.d (12)
La fracción irreducible es  .
.
Vemos que llegamos al mismo resultado que con el método anterior.
Vídeos explicativos
Ejemplo de vida real
Hemos comprado una pizza para cenar. Dividimos la pizza en 8 porciones iguales. Nos comemos 4 de ellas. Nos quedan 4 trozos. Representa la situación matemáticamente con fracciones y simplifícalas a su mínima expresión.
Resolución
Tenemos una pizza y la dividimos en 8 partes. La representación matemática con fracciones es  = 1
= 1
Cada porción se representa matemáticamente como 
Esta fracción ya no se puede reducir (el 1 y 8 no tienen ningún divisor en común salvo el 1), con lo cual  es fracción irreducible.
es fracción irreducible.
Si nos comemos 4 porciones de las 8, son  . Nos quedan 4 porciones de las 8, lo que es
. Nos quedan 4 porciones de las 8, lo que es  .
.
Veamos la fracción 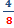 .
.
¿Se puede reducir? ¿Cuál sería la fracción irreducible?
Buscamos un divisor común de 4 y 8. Encontramos el número 2.
Dividimos tanto el numerador como el denominador a la vez entre 2
¿Tiene más divisores comunes? Vemos que tanto el 4 como el 8 se pueden dividir entre 2 de nuevo, con lo cual, volvemos a dividir el numerador y el denominador entre 2
Vemos que ya no se puede reducir más la fracción.
Nuestra fracción irreducible es 
Podemos comprobar que 
Nos hemos comido  de pizza y ha sobrado
de pizza y ha sobrado  .
.
Vemos lo importante que es reducir las fracciones.
¿Por qué decir cuatro octavos (4/8) cuando podemos decir un medio o lo que es lo mismo, la mitad (1/2)?
Cuatro octavos Dos cuartos Un medio
Enlaces de interés
No hay comentarios:
Publicar un comentario