Conceptos
Antes de empezar a dividir tenemos que valorar si queremos dividir dos fracciones o dividir números enteros entre fracciones, ya que el procedimiento variar un poco:
Dividir fracciones entre números enteros
Para dividir una fracción por un número entero hay que hacer 4 pasos:
Convertir el número entero en una fracción.
Encontrar el recíproco de esa fracción, es decir, darle la vuelta a la fracción.
Multiplicar el resultado por la primera fracción.
Simplificar la fracción (si hace falta).
Dividir dos fracciones
Para dividir fracciones hay que hacer 3 pasos:
Encontrar el recíproco de la segunda fracción (la fracción por la que queremos dividir), es decir, darle la vuelta a la segunda fracción.
Multiplicar la primera fracción por la fracción recíproca de la segunda.
Simplificar la fracción (si hace falta).
La fracción resultante tendrá:
Como numerador: el resultado de multiplicar el numerador de la primera por el denominador de la segunda.
Como denominador: el resultado de multiplicar el denominador de la primera por el numerador de la segunda.
Resolución
Dividir fracciones entre números enteros
¿Cómo se resuelve?
Paso 1:
Convierte 4 en una fracción. 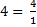 ;
;
Paso 2:
Dale la vuelta a la segunda fracción.
Paso 3:
Multiplica el resultado por la primera fracción.
Paso 4:
Simplifica la fracción.
¿Tiene 2 y 12 algún divisor común? Sí, tanto 2 como 12 se pueden dividir entre 2.
Además, 2 es m.c.d (máximo común divisor)
Divisores de 2: 1, 2
Divisores de 12: 1, 2, 3, 4, 6, 12
Resultado es: 
Dividir dos fracciones
¿Cómo se resuelve?
Paso 1:
Dale la vuelta a la segunda fracción
Paso 2:
Multiplica la primera fracción por la recíproca de la segunda:
Paso 3:
Simplifica la fracción.
¿Tienen 21 y 30 algún divisor en común? ¿Se pueden dividir entre 2? El 30 se puede dividir entre 2, pero el 21 no. ¿Se pueden dividir entre 3? Sí, los dos se pueden dividir entre 3.
Además, 3 es m.c.d (máximo común divisor)
Divisores de 21: 1, 3, 7 y 21
Divisores de 30: 1, 2, 3, 5, 6, 10, 15 y 30
Resultado es: 
Vídeo explicativo
Ejemplo de la vida real
María fue a la tienda a comprar 3 litros de crema que le hacían falta para preparar pasteles para su fiesta de cumpleaños. En la tienda sólo encontró bote de crema de ¼ de litro. María quiere saber cuántos botes debe comprar para tener los 3 litros que le hacen falta.
Resolución:
María necesita 3 litro de crema
En la tienda hay botes de  de litro.
de litro.
¿Cuántos botes tiene que comprar María para conseguir los 3 litros?
¿Cómo se resuelve?
Paso 1:
Convierte 3 en una fracción
Paso 2:
Dale la vuelta a la segunda fracción.
Fíjate que  se ha convertido en
se ha convertido en  ;
; 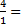 4
4
Recuerda que al principio hemos convertido el número entero 3 en fracción; 
Paso 3:
Multiplica la primera fracción por la recíproca de la segunda.
Como ves en el paso anterior, 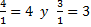 .
.
Podemos multiplicar directamente 3 x 4 = 12
A modo de revisión, repasamos el procedimiento completo:
El resultado es: María tiene que comprar 12 botes de crema.
Enlaces de interés
http://childtopia.com/index.php?module=videos&func=matematicas&seccion=matematicas&curso=p6&leccion=leccion5&playlist=4FF40DDE91970A8F&video=8PLR97udnWQ&idphpx=División de fracciones